Who thought we'd be modelling rope physics for the holidays?

What is Advent of Code?

In this little series, I want to write about the thought processes I have behind solving the puzzles presented in Advent of Code.

During the Advent of Code small coding puzzles are presented with varying levels of difficulty. They're always Christmas-themed text puzzles where you help elves out of some mess to save the holidays. The puzzles are deliberately ambiguous to not bias puzzlers into a certain solution, they always have an example input in the text to explain some details and an input file for each day that comes in the form of a text file you can download. The solution is a simple number or a string you enter, which is checked by the website automatically. After you finish part 1, part 2 unlocks, which is a variation on part 2. This can be a little twist on part 1 or a large twist that changes the problem formulation into a problem that would take brute force solutions to compute longer than the heat death of the universe would take.

Find my solutions here: github.com/JesperDramsch/advent-of-code

These descriptions won't be a perfect narrative, but rather how I think about these problems and where I see different solutions. I apologise for the possibility of rambling!

The example input

Whenever, I have to dig out the example input, I know it will be a brain twister!

R 4
U 4
L 3
D 1
R 4
D 1
L 5
R 2

at least we know that we're working with a 2D grid and a bunch of steps.

The implementation

2D grids always give me two intuitions.

First, use complex numbers to model the 2D plane and second use dictionaries to keep track of the locations.

This may be overkill in this on, since we're looking at a fairly linear and dense path of the rope head. Nevertheless, it's a data structure we can grow dynamically without too much hassle or memory constrains.

During the writing of the code, I realized that we're walking through the space and a set() is superior to a dict() for tracking visited squares.

The parsing was easy, I simply parsed everything into a complex number and an int.

def parse(data):
    directions = {"R": 1 + 0j, "L": -1 + 0, "U": 0 + 1j, "D": 0 - 1j}
    for line in data:
        direction, steps = line.split()
        yield directions[direction], int(steps)

The movement was tricky, since the lag between the head and the tail of the rope required some differencing and I initially calculated the movement of the tail using the head and a difference, but the tail needs to move independently and only based on its own position.

Then I fell into the usual trap that I like to fall in, which is that abs(1+1j) is not 1, so I need to be careful when check for distance between squares. A simple abs(diff) >= 2 does the trick here.

diff = tail - head
if abs(diff) >= 2:
    if diff.real != 0:
        tail = tail.real - (diff.real / abs(diff.real)) + tail.imag * 1j
    if diff.imag != 0:
        tail = tail.real + (tail.imag - (diff.imag / abs(diff.imag))) * 1j

I tried to be careful, debugging individual functions, to avoid off-by-one errors and weird behaviour. That resulted in me being fairly quick with my solution.

For the results, I used a fairly long print statement to see if the steps taken were correct. The formatting may seem overboard. However, this enabled me to find the error of not modeling the tail independently above in a single glance.

print(
    f"{int(head.real)} + {int(head.imag):d}j, \t {int(tail.real):d} + {int(tail.imag):d}j,\t {int(direction.real):d} + {int(direction.imag):d}j,\t {steps},\t {visited}"
)

Part Deux

Oh no. This is the point, where you stage the commit for day09.py maybe even commit just to be sure.

It seems like a smart choice that I modelled the movement independently, but it'll be interesting to see how to actually expand this to a dynamic 10-knot rope.

We also get a second sample input!

R 5
U 8
L 8
D 3
R 17
D 10
L 25
U 20

So…

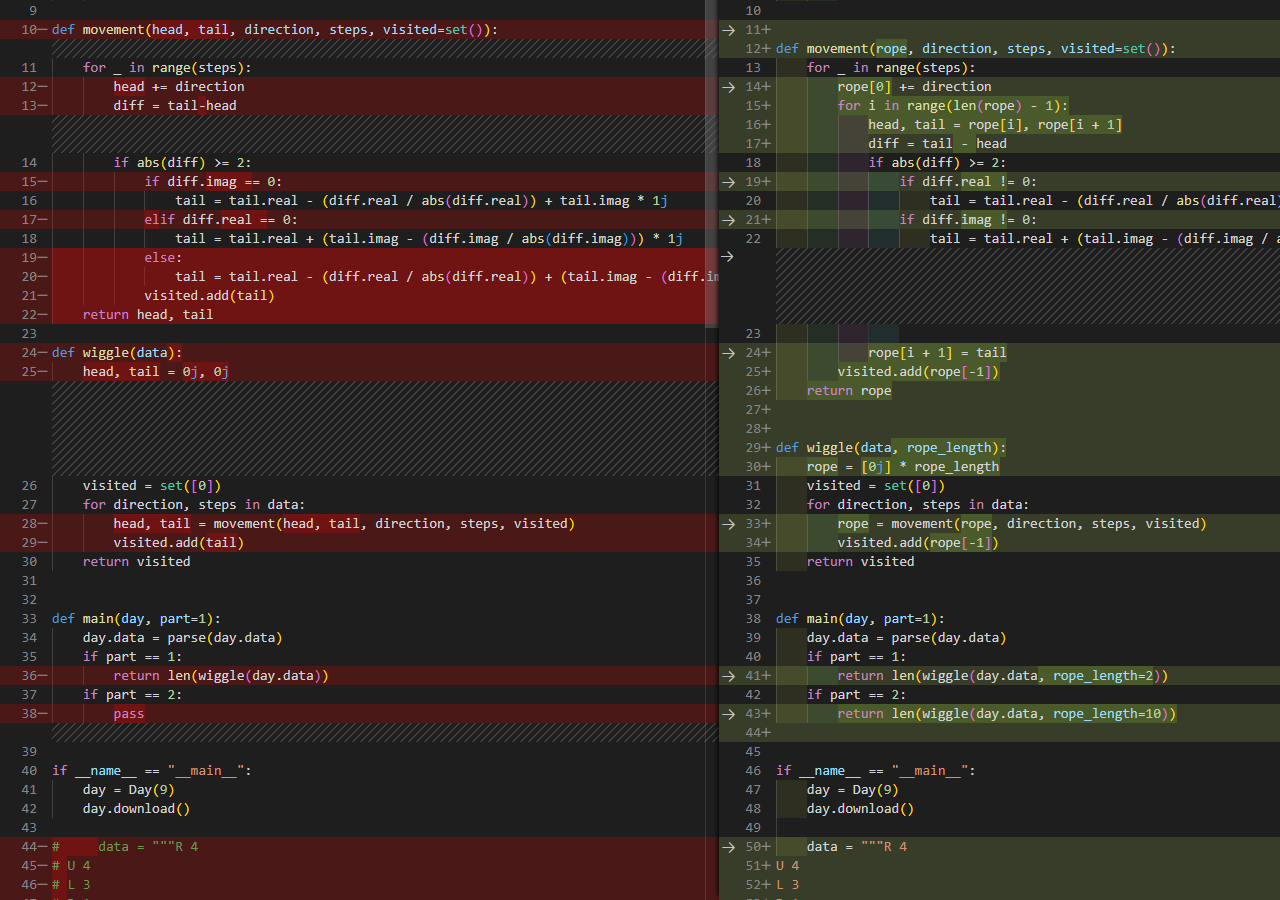
I don't want to hardcode the length, although we could. Our (head, tail) mini-rope will now become a neat little list.

Then I can still use the movement logic, but I iterate through the rope for each step instead!

for _ in range(steps):
    rope[0] += direction
    for i in range(len(rope) - 1):
        head, tail = rope[i], rope[i + 1]

And that worked out. Most of the logic stayed in place, I just figured out that I'm doing a comparison I don't need to make, so I changed:

if diff.imag == 0:
    tail = tail.real - (diff.real / abs(diff.real)) + tail.imag * 1j
elif diff.real == 0:
    tail = tail.real + (tail.imag - (diff.imag / abs(diff.imag))) * 1j
else:
    tail = (
        tail.real
        - (diff.real / abs(diff.real))
        + (tail.imag - (diff.imag / abs(diff.imag))) * 1j
    )

to a much cleaner:

if diff.real != 0:
    tail = tail.real - (diff.real / abs(diff.real)) + tail.imag * 1j
if diff.imag != 0:
    tail = tail.real + (tail.imag - (diff.imag / abs(diff.imag))) * 1j

I also think the diff is quite pleasant to look at:

Error Log

Fairly short error log for this one surprisingly, but I thing having more of a careful approach with print debugging and slowly building up each component helped here!

• day.data = parse(data) NameError: name 'data' is not defined oops. Forgot day..
• tail = head.real - (diff.real / abs(diff.real)) + (head.imag - (diff.imag / abs(diff.imag))) * 1j ZeroDivisionError: float division by zero didn't think about zeros...
• print(f"{head.real:d} + {head.imag:d}j, \t {tail.real:d} + {tail.imag:d}j,\t {direction.real:d} + {direction.imag:d}j,\t {steps},\t {visited}") ValueError: Unknown format code 'd' for object of type 'float' confused type conversion and formatting
• Conceptual error that I did not adjust the diagonal movement correctly.
• visited = set(0) TypeError: 'int' object is not iterable Can't start the set with just a zero
• tail = rope[i+1] IndexError: list index out of range gotta stop one before the end with pairs
• Made the error of using a for loop that returns items on a list that is changing... Didn't throw an error but gave the wrong result.