The Double Descent hypothesis is an interesting quirk of statistics and deep learning.
It explains why smalller models aren't always worse and larger models aren't always better.
Even worse... it shows that more data isn't always better!
Bias-Variance Trade-Off
A common topic in statistics is the bias-variance trade-off.
One way to look at this trade-off is that linear models are very robust against overfitting, considering they have two parameters. They often aren't enough to capture the complexity of a data set though. Once we increase the complexity we are better able to capture the training data, without regularization, however, these models will become highly attuned to the training data.
This also means that the model is less likely to generalize to unseen data. The model's capacity to overfit increases.
Classic Statistics
Classic statistics would expect an overly simple model is equally as bad as an over-parametrized model. Yet, there's a sweet spot in the middle of the parameter space.
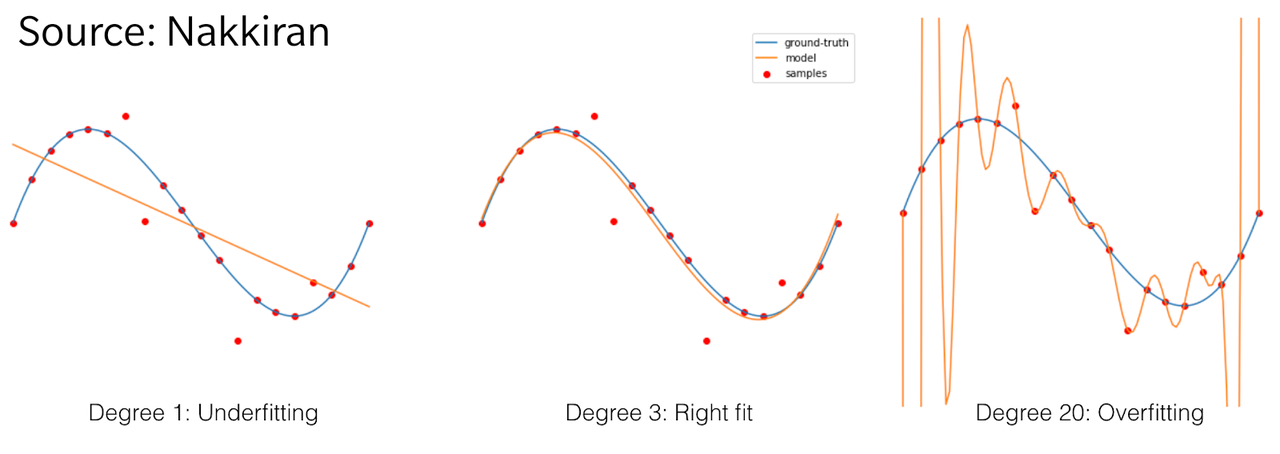
Think of a data distribution for x³ with some noise. A linear model would fit pretty bad, a quadratic model could at least fit half of a parabola, a cubic model is ideal to with the data, a fourth-order model with gets worse again similar to a parabola, and we get incrementally worse with higher-order models. When we get to models of orders equal to the number as samples, these start fitting directly to the noisy data points but wildly swing in between data points to try and hit them exactly. The common "overfitting"-image that gets used.
This is the first descent that minimizes the model error compared to model parameters in that center sweet spot.
Modern Machine Learning
Modern machine learning, however, presents an interesting contradiction to classic theory.
Highly over-parametrized models like neural networks... work. They work incredibly well at that. So well, in fact, that an infinitely wide multi-layer perception can be considered a universal function approximator. Large-scale models can do some incredible feats from self-driving cars to language understanding, well, at least part-ways there.
The second descent that minimizes the model error.
The Double Descent
We have a first descent in the classical statistics parameter space and another descent where modern neural networks live.
Clearly, you need a little bump in between our two descents, or it'd just be good ol' single descent and no hypothesis. That bump is arguably extra particularly interesting.
When we increase the size of a model to match the parameters with the samples of data, the model starts fitting exactly to any noise within the data.
Smaller models need to ignore much of the fluctuations in data, whereas, larger models can abstract much of the fluctuations. Only in that middle spot, where the models neither benefit from the inherent regularization of classical statistics, nor the over-parametrization, we see the error increase.
The Implications
This has a very interesting real implication. Since this is a deep connection between data complexity and model complexity, the makes model scaling very unintuitive from simple numbers alone.
It can happen that, due to the complexity of the data, when we increase the model size, we are still technically in a classical under-parameterized regime, despite having built a pretty massive model. We see the error increase, as we're still in the first descent. In the accompanying blog post, Nakkiran puts it as:
The take-away from our work (and the prior works it builds on) is that neither the classical statisticians’ conventional wisdom that “too large models are worse” nor the modern ML paradigm that “bigger models are always better” always hold.
Furthermore, it follows that more data is also not always better, as increasing the complexity of the data might push us on the local maximum between the double descent. Finishing out with:
These insights also allow us to generate natural settings in which even the age-old adage of “more data is always better” is violated!
Conclusion
Personally, I find this very insightful for some model debugging, where counter-intuitive behaviours of deep neural networks can be explained by their erratic behaviour right at this threshold between under- and over-parametrization.
The work on Double Descent was originally published in 2019 by Belkin et al. and then expanded on to Deep Double Descent by Nakkiran et al. from OpenAI. It was published on the OpenAI blog and Nakkiran goes more into depth on their blog. They're great reads, check them out
I write about these machine learning insights weekly in my newsletter.
